Dragon Curves

- plane filling curve

The classical Dragon curve, was discovered by physicist John E. Heighway. You can produce the curve by folding a long strip of paper in half several times, then unfolding all the creases to 90 degrees. It looks slightly like a dragon, hence its name.
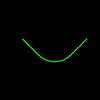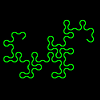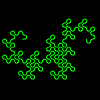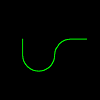
N folds result in an N-th order Dragon curve, with 2 Power N segments. Therefore the complexity of each stage increases exponentially. As a Dragon curve never intersects itself, it is a plane filling curve.

Recursively Generated Fractal Shape

The turtle draws the curve from one end to the other turning either left or right as necessary.
It calls the Dragon procedure recursivly, with either a positive (+1) or negative (-1) parity. This determines if the curve turns to the left or right by :Angle degrees.

A Dragon curve of order 0 is a straight line.
The limit for this curve is around order 13 (8192 segments), when the lines get too small (size 2).

To New
  # set default screen, pen and turtle values
  ResetAll SetScreenSize [400 400] HideTurtle
  SetSC Black SetPC Green SetPS 1 PenUp
End

To Init :Order
  # make Size and Angle global values
  Make "Size 11*Power (SqRt 2) (9-:Order)
  Make "Angle 90
End

To Display :Order
  # write header title and curve level
  SetPC White
  SetPos [-190 184] Label Sentence [Dragon Curve Order] :Order
End

To Dragon :Order :Parity
  If :Order < 1 [Forward :Size Stop]  # ie if = 0
  Dragon :Order-1 1
  Left :Parity*:Angle     # turn left or right :Angle degrees
  Dragon :Order-1 Minus 1
End

To Go :Order
  New
  Init :Order Display :Order
  SetPos [-108 0] SetPC Green PenDown
  Right (45 *:Order)+90     # similar orientations of curves
  Dragon :Order 1
End

Type Go order for example Go 5 to run.

For an animation of Dragon Curves of orders 0-11, add in the following procedure.

To GoX
  New Animation
  For [Order 0 11] [Wash     # comment out Wash for overlaid curves
  Init :Order Display :Order
    SetPos [-108 0] SetPC Green
    # SetPC 1 + Modulo :Order 2     # red or green
    PenDown Right (45 *:Order)+90     # similar orientations of curves
    Dragon :Order 1
    Refresh Wait 80 PenUp Home]
End

Four nested Dragon Curves using multi turtle mode, add in the following procedure.

To Init :Order
  # make Size and Angle global values
  Make "Size 9*Power (SqRt 2) (9-:Order)
  Make "Angle 90
End

To Go4 :Order
  New Init :Order Display :Order
  For [Turt 1 4] [
    SetTurtle :Turt SetPC :Turt PenDown
    Right (:Turt*90) + (45 *:Order)+45
    Dragon :Order 1 Wait 40]
End

Type go + order for example Go 5 to run.

Finally use this code for rounded corners. It makes the Dragon Curve easier to follow (it never intersects itself). Not so good with higher order curves.

To Init :Order
  # make Size and Angle global values
  Make "Size 11*Power (SqRt 2) (9-:Order)
  Make "Angle 90
  Make "Step 0.025*Pi * :Size Make "Ang :Angle/10
End

To Turn :A
  Left :A/2
  Repeat 9 [Forward :Step Left :A]
  Forward :Step Left :A/2
End

To Dragon :Order :Parity
  If :Order < 1 [Stop]     # ie if = 0
  Dragon :Order-1 1
  Turn :Parity*:Ang     # turn left or right :Angle degrees
  Dragon :Order-1 Minus 1
End

To Go :Order
  New
  Init :Order Display :Order
  SetPos [-108 0] SetPC Green PenDown
  Right (45 *:Order)+90     # similar orientations of curves
  Forward :Size/2 Dragon :Order 1 Forward :Size/2
End

Type Go order for example Go 5 to run.

Dragon Curve
Dragon Curve

 

Dragon Curves
DC order 0-9

Procedures blue
Variables pink
Comments green
Library gray